How to Factor Quadratic Functions

Quadratic functions are a type of polynomial function where the highest exponent is 2. They can be written in several different forms, and each form highlights different information.

In this post, we’ll focus on quadratics written in standard form:

f(x) = ax² + bx + c, where a ≠ 0

When quadratics are written in this way, we can find their x-intercepts (also called roots or zeros) using different solving methods:

• Factoring

• Quadratic Formula

• Completing the Square

• Square Root Method

We’ll cover all of these in future lessons, but today we’ll focus on factoring.

Remember: Solving a quadratic means finding the x-values where the graph crosses the x-axis. A quadratic can have 0, 1, or 2 x-intercepts.

---

Want extra practice? Check out our Quadratics: Solving by Factoring Guided Notes & Practice Sets or on TPT for step-by-step notes, worksheets, and answer keys.

---

Case 1: Factoring When There Is No “c” Term

If the quadratic looks like:

f(x) = ax² + bx, where a ≠ 0

then the constant term c = 0. In this case, we can factor by taking out the Greatest Common Factor (GCF).

Factoring Out the GCF

The GCF is the largest factor shared by all terms—both the numbers (coefficients) and the variables.

Example:

f(x) = 2x² + 8x

• Coefficient GCF: between 2 and 8 → 2

• Variable GCF: between x² and x → x

So the overall GCF is 2x.

Now factor it out:

f(x) = 2x² + 8x = 2x(x + 4)

You can always check by distributing back to the original form.

---

Case 2: Factoring When a = 1

If the quadratic looks like:

f(x) = x² + bx + c

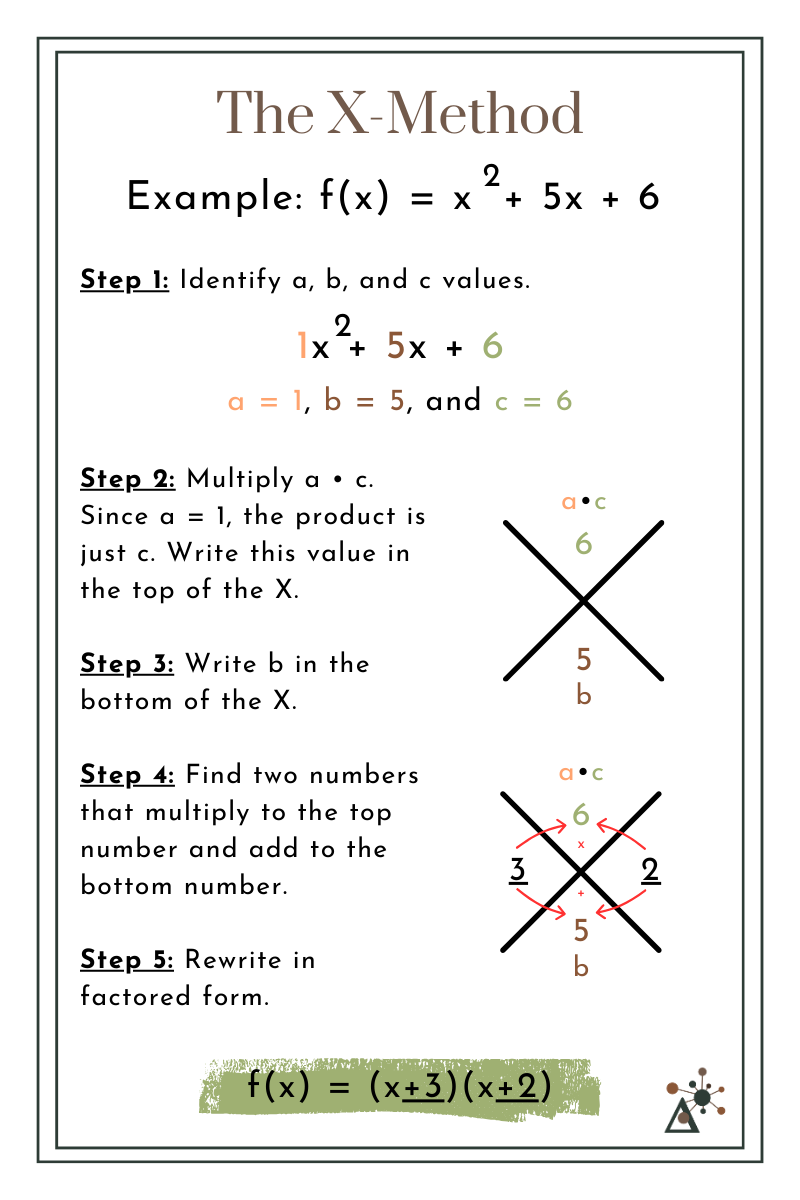
we can use the X-Method.

The X-Method

1. Identify the a, b, and c values.

2. Multiply a • c. Since a = 1, the product is just c. Write this value in the top of the X.

3. Write b in the bottom of the X.

4. Find two numbers that multiply to the top number and add to the bottom number.

5. Rewrite in factored form.

Example:

y = x² + 5x + 6

a = 1, b = 5, and c = 6

• Top of the X: 1 ⋅ 6 = 6

• Bottom of the X: b = 5

• Factor pair: 2 and 3 (since 2 ⋅ 3 = 6 and 2 + 3 = 5)

So,

y = (x + 2)(x + 3)

---

Case 3: Factoring When a ≠ 1

If a is not equal to 1, factoring takes an extra step. Two common approaches are:

• The Box Method

• The Grouping Method

Both start with the same first step: multiply a ⋅ c.

---

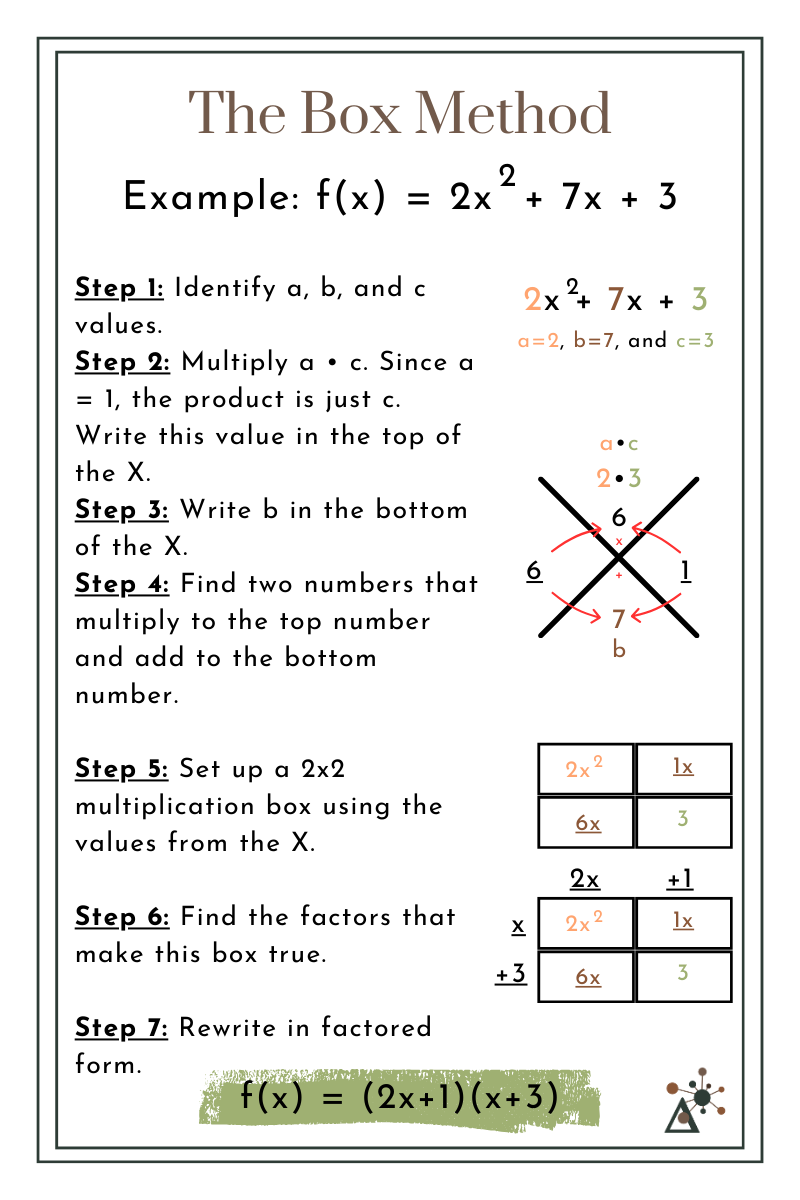
The Box Method

Example:

y = 2x² + 7x + 3

a = 2, b = 7, and c = 3

• Multiply: a ⋅ c = 2 ⋅ 3 = 6

• Find the two numbers that multiply to 6 and add to 7 → 6 and 1

Now set up a 2×2 multiplication box:

	2x	+1
x	2x2	1x
+3	6x	3

The factors that make this box work are:

(x + 3) and (2x + 1)

Our final factored form will be:

y = (x + 3)(2x + 1)

---

The Grouping Method

Using the same example:

y = 2x² + 7x + 3

1. Multiply a⋅c = 6, and find numbers that multiply to 6 and add to 7 → 6 and 1.

2. Rewrite the middle term (7x) as 6x +1x. The coefficients are the values found in Step 1.

y = 2x² + 6x + 1x + 3

3. Group and factor each part:

y = (2x² + 6x) + (1x + 3)

y = 2x(x+3) + 1(x+3)

4. Factor out the common binomial:

(2x + 1)(x + 3)

---

Conclusion

Factoring quadratics is one of the most useful methods for finding x-intercepts. Which method you use depends on the structure of the quadratic:

• Factoring out the GCF (when c = 0)

• The X-Method (when a = 1)

• The Box Method (when a ≠ 1)

• Grouping (when a ≠ 1)

In our next posts, we’ll explore special factoring patterns like:

• Perfect Square Trinomials

• Difference of Squares

These patterns make factoring even faster!