Find The Domain and Range of Continuous Functions
In our last lesson, we talked about the difference between relations and functions. Now, let’s build on that by learning how to describe the domain and range of a function. Being precise with notation is important, because domain and range tell us exactly what values a function can take.
If you would like a refresher on relations and functions, check out our previous blog here!
Key Vocabulary
Domain → the set of all possible x-values (inputs).
Range → the set of all possible y-values (outputs).
If a function can take all real values, we write this as:
Interval notation: (−∞,∞)
Set notation: ℝ (symbol stands for all real values)
Interval Notation: A Compact Way to Write Sets
Interval notation uses parentheses ( ) and brackets [ ] to describe a continuous stretch of numbers.
( ) means the endpoint is not included.
[ ] means the endpoint is included.
For example, let’s take a look at the following continuous function example:
Example Function:
$$f(x) = -x^2, \quad x < 2$$
Because the domain of a graph stretches left forever but stops at x=2 (and does not include 2), we write:
(−∞ , 2)
If the range of the graph extends downward forever but has a maximum value of y=0, and that maximum is included, we write:
(−∞ , 0]
Extra Note on Parentheses and Brackets
You don’t always have to use the same type of symbol on both ends of an interval. Depending on the graph’s behavior, you might see something like (,] or [,). For example, if the minimum value is included but the maximum is not, you would write [a,b).
Also remember: whenever an interval extends to +∞ or −∞, you must use a parenthesis, never a bracket, because infinity is not an actual number we can include.
Inequality Notation: Another Way to Write the Same Idea
Inequality notation uses <, >, ≤, and ≥ to describe values.
The same domain above can be written as:
x < 2
The same range becomes:
y ≤ 0
Both notations mean the same thing—you just have two different tools to describe sets of numbers.
Non-Continuous Functions and Union Notation
Not all functions are smooth curves! Sometimes a function is piecewise, meaning it is made of different “pieces” on different intervals. In these cases, the domain and range might not be one continuous interval.
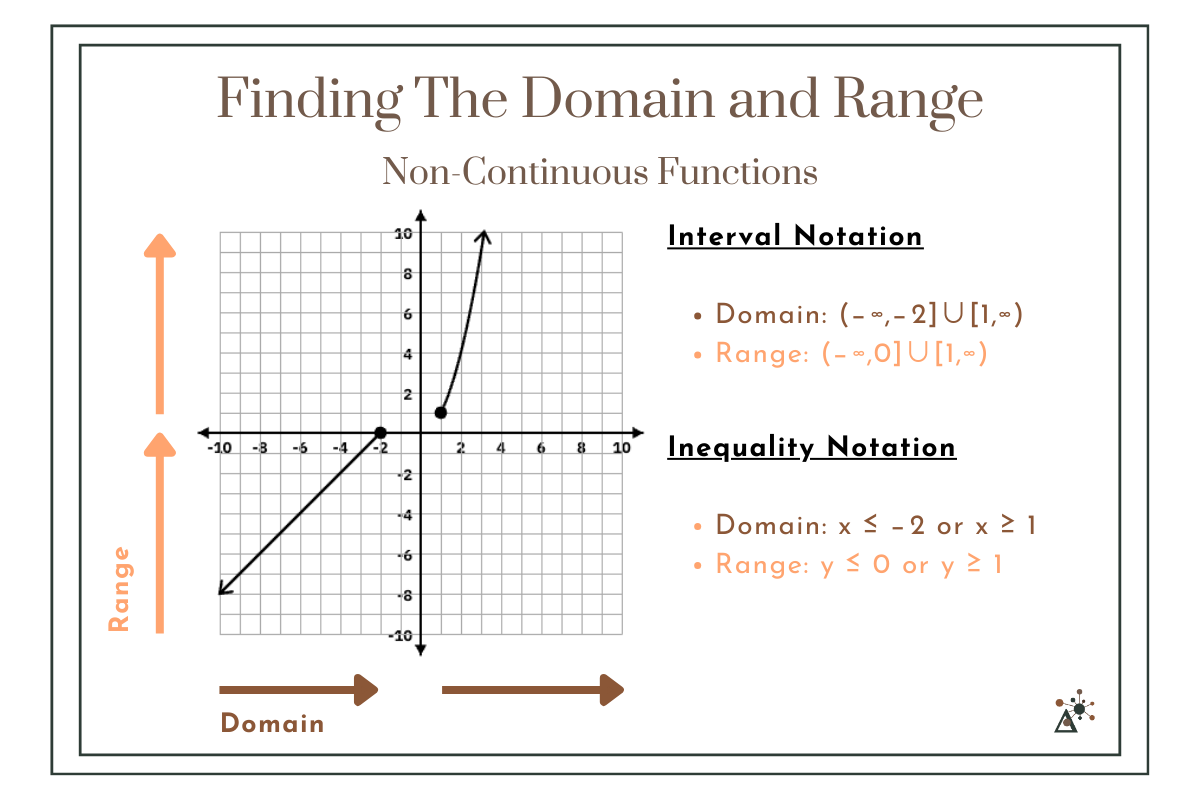
Example: Non-Continuous Piecewise Function
We define the function:
$$f(x)= \begin{cases} x+2, & x \leq -2 \\ x^2, & x \geq 1 \end{cases}$$
For the domain:
From the first piece, we have all x ≤ −2 or (−∞,−2].
From the second piece, we have all x ≥ 1, or [1,∞).
Since the function is defined in two separate intervals, we connect them with a union symbol ( ∪ ):
(−∞ , −2] ∪ [1 , ∞)
For the range:
From the first piece (x + 2), the outputs go all the way down to −∞, and the largest value occurs when x = −2, giving y = 0. So this part of the range is (−∞ , 0].
From the second piece (x^2), the outputs are all y ≥ 1, or [1 , ∞).
Putting them together:
(−∞ , 0] ∪ [1 , ∞)
Common Mistakes to Avoid
Forgetting about all real numbers. If a graph extends in both directions forever, don’t stop at a random value. Write (−∞,∞) or ℝ.
Mixing up domain and range. Remember: domain = x-values (horizontal), range = y-values (vertical).
Dropping parts of piecewise functions. Always check each piece and use union notation ( ∪ ) if needed.
Using brackets incorrectly. Open circles and arrows → ( or ). Closed circles and exact max/min → [ or ].
Whether you use interval or inequality notation, always start with the smallest values and move toward the largest. Precision is key!