Rules for Significant Figures
What Are Significant Figures?
Definition
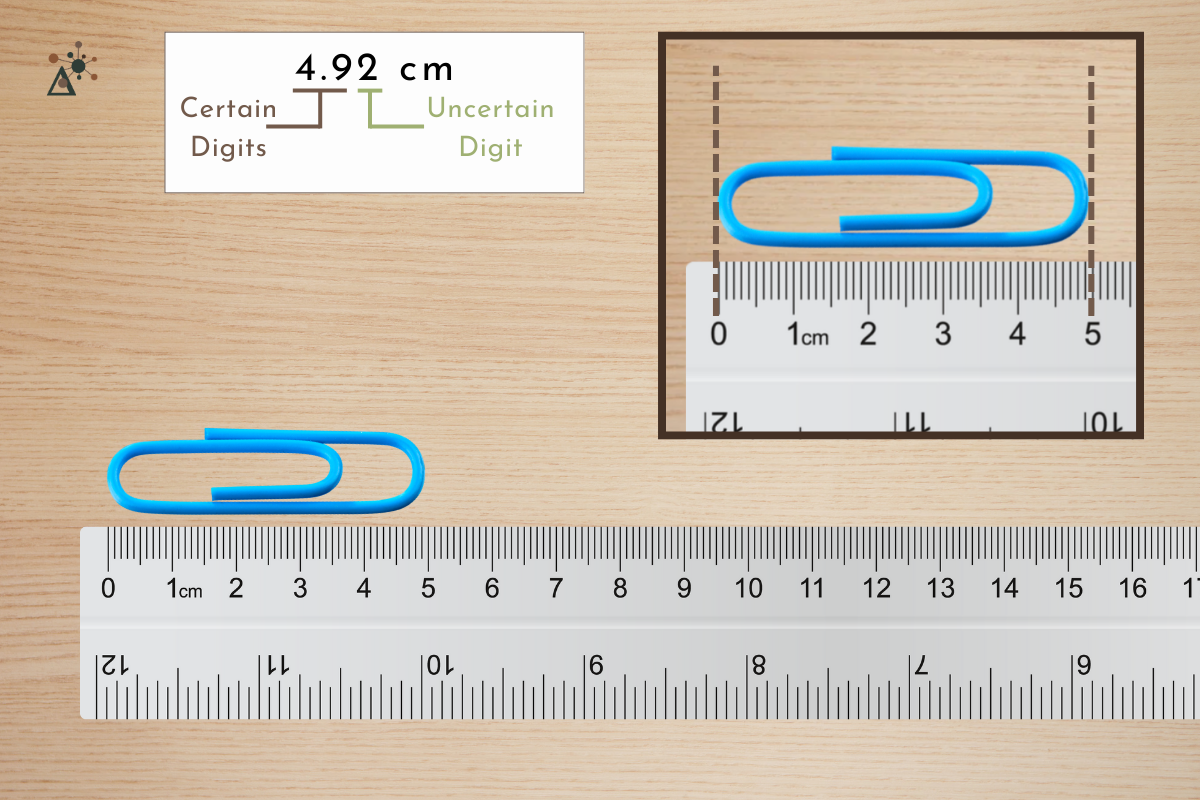
Significant figures (often called sig figs and abbreviated s.f.) represent the precision of a measurement. They tell us which digits in a number are known with certainty, plus the one digit that is an estimate, or uncertain.
Example: When using a ruler, you can be certain about the digits that line up with the markings, but the very last digit—the one you estimate between two markings—is uncertain. This final digit is still significant, but not completely certain.
Rules for Counting Significant Figures
All non-zero digits are always significant.
Example 1: 34.5 → 3 sig figs
Example 2: 41.9234 → 6 sig figs
Zeroes between non-zero digits are significant.
Example 1: 2002 → 4 sig figs
Example 2: 0.1203 → 4 sig figs
Leading zeroes (before the first non-zero digit) are not significant.
Example 1: 0.0007 → 1 sig fig
Example 2: 0.9 → 1 sig fig
Trailing zeroes (after the last non-zero digit) may or may not be significant.
Example 1: 8400 → 2 sig figs (no decimal shown, so trailing zeroes aren’t significant)
Example 2: 1.28900 → 6 sig figs (decimal point makes trailing zeroes significant)
Example 3: 8400.0 → 5 sig figs
Note: Trailing zeroes are significant when a decimal point is present.
Exact numbers have unlimited significant figures.
Example 1: 1 foot = 12 inches (a defined relationship, infinite sig figs)
Example 2: 6.02214076 × 10²³ molecules (a counted or defined value, infinite sig figs)
Rules for Adding and Subtracting
When adding or subtracting, your answer should be rounded to the same number of decimal places as the measurement with the fewest decimal places.
Example 1: 0.07 + 2.305 = 2.38 (2 decimal places)
Example 2: 113.9 − 2.1035 = 111.8 (1 decimal place)
s.f = significant figures
Rules for Multiplying and Dividing
When multiplying or dividing, your answer should have the same number of significant figures as the measurement with the fewest significant figures.
Example 1: 204.3 × 6.5 = 1300 or 1.3 × 10³ (2 sig figs)
Example 2: 327.506 ÷ 1.34 = 244 (3 sig figs)
Conclusion
Significant figures keep our measurements honest—they show the level of precision in science and prevent us from claiming more certainty than our tools allow. By applying these rules, you’ll always know how to properly record and calculate with your data.
📥 Want a quick reference? [Download the Significant Figures Rules PDF here!]